การวิเคราะห์ความต้านทาน ความต้านทานอินพุต และความต้านทานเอาต์พุต

อิมพีแดนซ์เป็นคำเรียกรวมสำหรับความต้านทานและรีแอกแตนซ์ และความแตกต่างที่ใหญ่ที่สุดระหว่างความต้านทานและรีแอกแตนซ์ก็คือ ความต้านทานกระแสจำกัด (กฎของโอห์ม) ใช้พลังงานไฟฟ้าในเวลาเดียวกัน รีแอกแตนซ์จำกัดอยู่ที่กระแสและไม่สิ้นเปลืองพลังงานไฟฟ้า (โดยไม่ต้องทำงาน) ความต้านทานมีผลกระทบต่อกระแสไฟฟ้าที่จำกัดทั้งในกระแสตรงและกระแสสลับ ในขณะที่รีแอกแตนซ์มีผลกับกระแสไฟฟ้าที่จำกัดในสภาพแวดล้อมกระแสสลับเท่านั้น

อิมพีแดนซ์อินพุตหมายถึงอิมพีแดนซ์ที่เท่ากันที่ปลายอินพุตของวงจร เพิ่มแหล่งจ่ายแรงดันไฟฟ้า U ไปที่เทอร์มินัลอินพุตและวัดกระแส I ที่เทอร์มินัลอินพุต จากนั้นอิมพีแดนซ์อินพุต Rin คือ U/I คุณสามารถจินตนาการว่าปลายอินพุตเป็นปลายทั้งสองของตัวต้านทาน และค่าความต้านทานของตัวต้านทานนี้คืออิมพีแดนซ์อินพุต

ภายใต้แรงดันไฟฟ้าอินพุตเดียวกัน หากอิมพีแดนซ์อินพุตต่ำมาก กระแสไฟฟ้าขนาดใหญ่จำเป็นต้องไหล ซึ่งจะทดสอบความสามารถเอาต์พุตปัจจุบันของสเตจก่อนหน้า หากอิมพีแดนซ์อินพุตสูง จะต้องใช้กระแสเพียงเล็กน้อยเท่านั้น ซึ่งจะช่วยลดภาระที่สำคัญต่อความสามารถเอาท์พุตปัจจุบันของสเตจด้านหน้า ดังนั้นในการออกแบบวงจร พยายามเพิ่มอิมพีแดนซ์อินพุตให้มากที่สุด

อิมพีแดนซ์อินพุตไม่แตกต่างจากส่วนประกอบรีแอกแตนซ์ทั่วไป เนื่องจากสะท้อนขนาดของเอฟเฟกต์การบล็อกในปัจจุบัน

สำหรับวงจรที่ขับเคลื่อนด้วยแรงดันไฟฟ้า ยิ่งอิมพีแดนซ์อินพุตมากขึ้น โหลดบนแหล่งจ่ายแรงดันไฟฟ้าก็จะยิ่งเบาลง ทำให้ขับได้ง่ายขึ้นโดยไม่กระทบต่อแหล่งสัญญาณ สำหรับวงจรที่ขับเคลื่อนด้วยกระแส ยิ่งอิมพีแดนซ์อินพุตมีค่าน้อย โหลดบนแหล่งกำเนิดกระแสก็จะยิ่งเบาลง

ดังนั้น เราสามารถคิดได้ว่าถ้าใช้แหล่งกำเนิดแรงดันไฟฟ้าในการขับเคลื่อน ยิ่งอิมพีแดนซ์อินพุตมากเท่าไรก็ยิ่งดีเท่านั้น ถ้าขับเคลื่อนโดยแหล่งกำเนิดกระแส ยิ่งอิมพีแดนซ์น้อยก็ยิ่งดี (หมายเหตุ: เหมาะสำหรับวงจรความถี่ต่ำเท่านั้น ในวงจรความถี่สูง ควรพิจารณาการจับคู่อิมพีแดนซ์ด้วย) นอกจากนี้ เมื่อได้รับกำลังเอาต์พุตสูงสุด อิมพีแดนซ์ ควรพิจารณาการจับคู่ด้วยความต้านทานเอาต์พุต

อิมพีแดนซ์เอาต์พุตประกอบด้วยอิมพีแดนซ์ภายในของแหล่งแรงดันไฟฟ้าที่เทียบเท่า (วงจรเทียบเท่า Thevenin) หรือแหล่งกระแสเทียบเท่า (วงจรเทียบเท่า Norton) ของพอร์ตเอาต์พุตเครือข่ายพลังงานอิสระ ค่าของมันเท่ากับอิมพีแดนซ์อินพุตที่เห็นจากพอร์ตเอาต์พุตเมื่อตั้งค่าแหล่งจ่ายไฟอิสระเป็นศูนย์

ไม่ว่าแหล่งสัญญาณ แอมพลิฟายเออร์ และพาวเวอร์ซัพพลายจะเป็นอย่างไร ก็มีปัญหากับอิมพีแดนซ์เอาต์พุต ความต้านทานเอาต์พุตคือความต้านทานภายในของแหล่งสัญญาณ เดิมที สำหรับแหล่งจ่ายแรงดันไฟฟ้าในอุดมคติ (รวมถึงแหล่งจ่ายไฟ) ความต้านทานภายในควรเป็น 0 หรืออิมพีแดนซ์ของแหล่งจ่ายกระแสในอุดมคติควรเป็นอนันต์ อิมพีแดนซ์เอาต์พุตต้องการความสนใจเป็นพิเศษในการออกแบบวงจร

ในความเป็นจริง แหล่งจ่ายแรงดันไฟฟ้าไม่สามารถบรรลุสิ่งนี้ได้ และแหล่งจ่ายแรงดันไฟฟ้าในอุดมคติมักจะเชื่อมต่อแบบอนุกรมกับตัวต้านทาน r เพื่อให้เทียบเท่ากับแหล่งจ่ายแรงดันไฟฟ้าจริง ตัวต้านทาน r ในอนุกรมที่มีแหล่งจ่ายแรงดันไฟฟ้าในอุดมคติคือความต้านทานภายในของแหล่งสัญญาณ/เอาต์พุตของเครื่องขยายสัญญาณ/แหล่งจ่ายไฟ

เมื่อแหล่งจ่ายแรงดันไฟฟ้านี้จ่ายพลังงานให้กับโหลด กระแส I จะไหลผ่านโหลดและสร้าง I บนตัวต้านทานนี้ × แรงดันตกคร่อมของ r ซึ่งจะส่งผลให้แรงดันไฟฟ้าเอาท์พุตของแหล่งจ่ายไฟลดลง ซึ่งจะจำกัดกำลังไฟฟ้าเอาท์พุตสูงสุด

ในทำนองเดียวกัน แหล่งกำเนิดกระแสในอุดมคติควรมีอิมพีแดนซ์เอาต์พุตเป็นอนันต์ แต่วงจรจริงนั้นเป็นไปไม่ได้

อิมพีแดนซ์เอาท์พุตหมายถึงอิมพีแดนซ์ที่เท่ากันของวงจรเมื่อโหลดวงจรถูกมองจากพอร์ตเอาท์พุตของวงจรในทิศทางตรงกันข้าม ในความเป็นจริง ส่วนใหญ่หมายถึงอิมพีแดนซ์ที่วัดโดยแหล่งพลังงานที่ปลายเอาต์พุต หรือที่เรียกกันทั่วไปว่าความต้านทานภายใน

การวิเคราะห์การคิดอิมพีแดนซ์ของวงจรสวิตชิ่ง

ดังแสดงในรูปต่อไปนี้ V1 ยังคงส่งกระแสไปที่ R1 และวงจรกระแสในรูปจะแสดงด้วยลูกศรสีเขียว เรามีวิธีการอะไรบ้างหากต้องการควบคุมกระแสไหลไปที่ R1?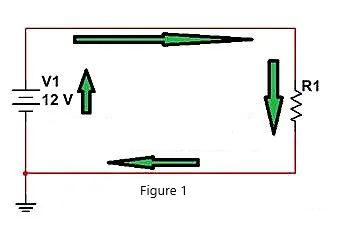

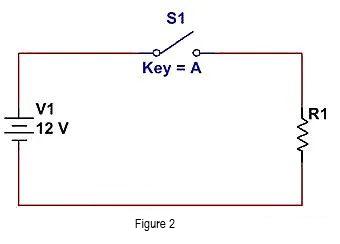
วิธีที่พบบ่อยที่สุดคือตัดการเชื่อมต่อระหว่าง V1 และ R1 แล้วตัดวงจรกระแสไฟออก ดังแสดงในรูปต่อไปนี้

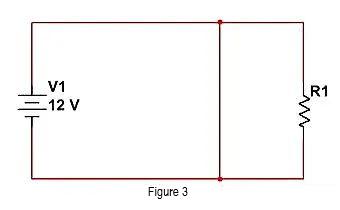
หรืออีกทางหนึ่งเราสามารถเลี่ยงผ่าน R1 ได้ดังแสดงในรูปต่อไปนี้ เพิ่มสายไฟไว้ด้านหน้า R1 เพื่อส่งกระแสไฟฟ้าไปยังเส้นทางที่มีอิมพีแดนซ์ต่ำ และ R1 จะได้รับกระแสไฟฟ้าเพียงเล็กน้อย

สองวิธีข้างต้นนั้นตรงไปตรงมามาก ไม่ว่าจะเป็นการตัดการเชื่อมต่อเส้นทางจาก V1 ไปยัง R1 โดยสิ้นเชิงหรือการลัดวงจร R1 ซึ่งช่วยแก้ปัญหาได้อย่างละเอียด แต่ในโลกของวิศวกรรม เราไม่สามารถทำได้อย่างหมดจดและเรียบร้อยขนาดนี้ โดยมักจะเน้นย้ำถึงสิ่งที่ "คล้ายกัน" เข้าใกล้. ดังนั้นใน "รุ่นลัดวงจร" เราทำได้เพียง "ความต้านทานต่ำ" ในขณะที่ใน "รุ่นวงจรเปิด" เราทำได้เพียง "ความต้านทานสูง" เท่านั้น หากพลังงาน "ลดทอน" ลงอย่างมาก เราเชื่อว่าเป็นไปตามมาตรฐาน

ดังแสดงในรูปด้านล่าง แบบจำลองโหลดกำลังจริงจะแสดงขึ้น มาดูวิธีการเปลี่ยนเอฟเฟกต์โดยการปรับอิมพีแดนซ์ ในวงจรจริง แหล่งพลังงานมีข้อจำกัดด้านความจุเอาท์พุตและความต้านทานภายใน และยิ่งกระแสไฟเอาท์พุตมากขึ้น แรงดันไฟเอาท์พุตก็จะยิ่งต่ำลง

วงจรต่อไปนี้มีความต้านทานภายใน 0.1 Ω และโหลด 1K Ω ในสถานการณ์ปัจจุบัน แรงดันไฟฟ้าที่ได้รับที่ปลายทั้งสองของโหลดจะประกอบด้วยความต้านทานภายในและแรงดันไฟฟ้าย่อย R2 เราสามารถคำนวณ V=5V * (1K/(1K+0.1))=4.9999V, I=5V/1000.1 Ω=4.9mA

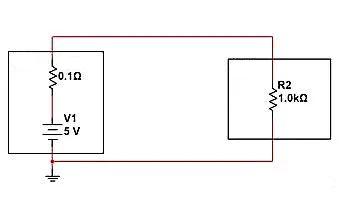
หากเราใช้ "โมเดลวงจรเปิด" วิธีตัดวงจร เราควรปรับ Impedance อย่างไร? เป็นการเชื่อมต่อตัวต้านทานที่มีค่ามากกว่า 1K มากเป็นอนุกรมระหว่างแหล่งจ่ายไฟและโหลด และดำเนินการแบ่งแรงดันไฟฟ้าแบบอนุกรมเพื่อลดแรงดันไฟฟ้าที่ได้รับบน R2 ดังแสดงในรูปต่อไปนี้ หากเชื่อมต่อตัวต้านทาน 1M แบบอนุกรมกับตัวแบ่งแรงดันโหลด เราสามารถคำนวณการกระจายแรงดันไฟฟ้าขั้นสุดท้ายระหว่างปลายทั้งสองของโหลดได้:

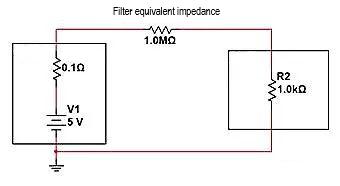
วี=5V * (1K/(0.1+1,000K+1K))=0.00499V, I=5V/1001000.1 Ω=0.0049mA แอมพลิจูดลดลงเกือบ 1,000 เท่า และในการคิดทางวิศวกรรม R2 เกือบจะ "ขาดการเชื่อมต่อ"

หากเราใช้ "รูปแบบการลัดวงจร" วิธีถอด R2 เราควรปรับยังไง? เป็นการเชื่อมต่อตัวต้านทานที่มีขนาดเล็กกว่า 0.1 Ω ขนานกันที่ปลายด้านหน้าของโหลด และดำเนินการแบ่งปันแรงดันไฟฟ้าแบบอนุกรมกับตัวต้านทานภายใน ส่งผลให้แรงดันไฟฟ้าที่ได้รับบน R2 น้อยลง

ดังแสดงในรูปต่อไปนี้ หากการวัดการกรองเทียบเท่ากับตัวต้านทานแบบขนาน 0.005 Ω และตัวแบ่งแรงดันไฟฟ้าความต้านทานภายใน เราสามารถคำนวณแรงดันไฟฟ้าแบบกระจายสุดท้ายระหว่างปลายทั้งสองของโหลด R2 ได้:

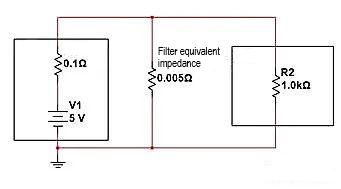
V=5V * (0.0049/(0.1+0.0049)=0.233V แอมพลิจูดลดลงเกือบ 20 เท่า และในการคิดทางวิศวกรรม R2 ก็คล้ายกับการ "ขาดการเชื่อมต่อ"

ข้างต้นเป็นแบบจำลองทางทฤษฎีของวงจรสวิตช์เซมิคอนดักเตอร์ โดยใช้วงจรอินเวอร์เตอร์เป็นตัวอย่าง:

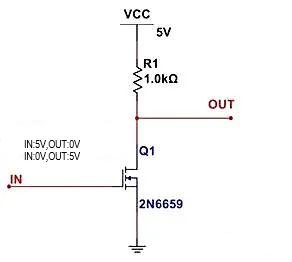
เมื่อปลาย IN ถูกขับเคลื่อน เราจะบอกว่าทรานซิสเตอร์ MOS Q1 กำลังดำเนินการอยู่ ณ จุดนี้ สถานะการนำไฟฟ้าจะเทียบเท่ากับการที่ Q1 กลายเป็นตัวต้านทานที่มีอิมพีแดนซ์หลายสิบมิลลิโอห์ม จากนั้นจึงแบ่งแรงดันไฟฟ้าด้วยตัวต้านทาน R1 หากตัวต้านทานแบบดึงขึ้น R1 มีขนาดเล็กเกินไปและมีค่าหลายสิบมิลลิโอห์มด้วย แม้ว่า IN จะสูงและ Q1 กำลังดำเนินการอยู่ ขั้วต่อ OUT จะไม่สามารถเอาต์พุตระดับต่ำได้

เมื่อปลาย IN ถูกปิด เราจะบอกว่าทรานซิสเตอร์ MOS Q1 ถูกตัดออก ณ จุดนี้ สถานะจุดตัดจะเทียบเท่ากับการที่ Q1 กลายเป็นตัวต้านทานที่มีอิมพีแดนซ์ไม่กี่เมกะโอห์ม และแบ่งแรงดันไฟฟ้าด้วยตัวต้านทาน R1 หากตัวต้านทานแบบดึงขึ้น R1 มีขนาดใหญ่เกินไป ซึ่งมีไม่กี่เมกะโอห์มเช่นกัน แม้ว่า IN จะต่ำและ Q1 ถูกตัดออก ขั้วต่อ OUT จะไม่สามารถเอาต์พุตในระดับสูงได้

ดังนั้นเมื่อเข้าใจวงจรสวิตช์อย่างลึกซึ้ง จำเป็นต้องวิเคราะห์วงจรเหล่านั้นด้วยการคิดเกี่ยวกับอิมพีแดนซ์

วงจรกรองการวิเคราะห์การคิดอิมพีแดนซ์

ที่นี่ วิเคราะห์วงจรการกรองโดยใช้การคิดอิมพีแดนซ์

ในการใช้งานจริงทางวิศวกรรม กำลังไฟฟ้าเอาท์พุตมักประกอบด้วยส่วนประกอบ AC ที่มีความถี่ต่างกัน ทั้งที่เราต้องการและที่เราไม่ต้องการ ความต้านทานของการเหนี่ยวนำและความจุจะแตกต่างกันไปตามความถี่ เป็นเพราะลักษณะนี้เองที่ทำให้ตัวเหนี่ยวนำและตัวเก็บประจุกลายเป็นตัวแสดงชั้นนำในวงจรกรอง

ยังคงใช้วงจรต่อไปนี้ โดยสมมติว่าแหล่งจ่ายไฟมีส่วนประกอบสเปกตรัมของ
0-1GHz.

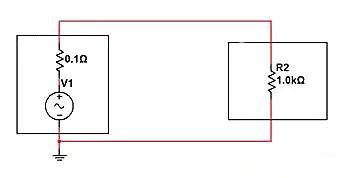
หากเราต้องการกรองส่วนประกอบ AC ความถี่สูงสำหรับโหลด R2 เราจะพบว่าทั้งการเหนี่ยวนำแบบอนุกรมและความจุแบบขนานสามารถตอบสนองความต้องการได้
ดังแสดงในรูปต่อไปนี้ หากตัวเหนี่ยวนำ 16uH หนึ่งตัวเชื่อมต่อแบบอนุกรมระหว่างแหล่งจ่ายไฟและโหลด ส่วนประกอบ AC 100MHz จะสลายตัวเป็นเท่าใด ตามสูตรอิมพีแดนซ์ของการเหนี่ยวนำ: ZL=2 π fL=2 * 3.14 * 100MHz * 16uH, สามารถรับ ZL=10K ได้

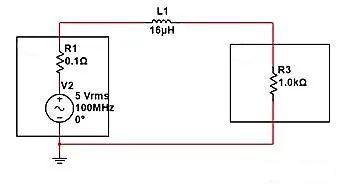
ตามสูตรตัวแบ่งแรงดันไฟฟ้าแบบอนุกรม แรงดันไฟฟ้า/อินพุตที่ปลายทั้งสองของ R3=R3/(R3+ZL)=1K/11K=0.0909 ดังนั้นเมื่อแอมพลิจูดของแหล่งจ่ายไฟคือ 5V แอมพลิจูดที่ปลายทั้งสองของ R3 จะเท่ากับ 5V * 0.0909=0.45V

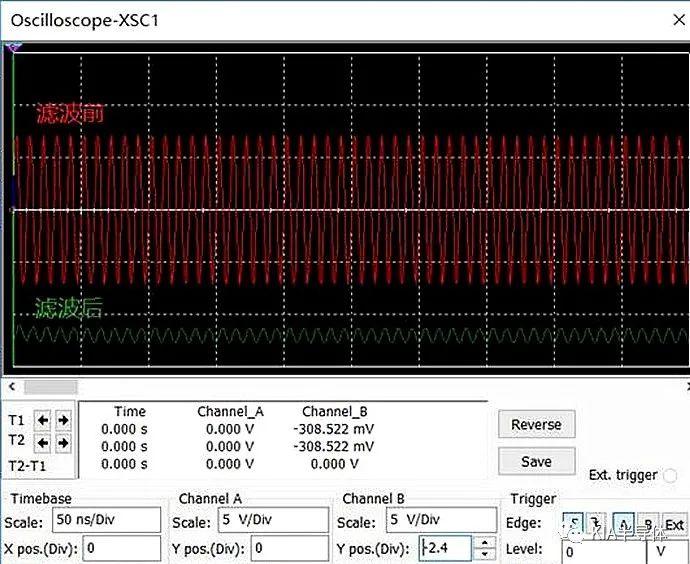
ที่ความถี่ 100MHz ให้ใช้ออสซิลโลสโคปเพื่อวัดรูปคลื่นก่อนและหลังการกรอง การเปรียบเทียบแสดงให้เห็นว่ารูปคลื่น 100MHz มีผลกระทบ และการวัดจริงคือ 0.449V ซึ่งสอดคล้องกับผลการวิเคราะห์

การวิเคราะห์การคิดอิมพีแดนซ์ของฟิลเตอร์โลว์พาส

โดยการเชื่อมต่อตัวเหนี่ยวนำแบบอนุกรมระหว่างแหล่งจ่ายไฟและโหลด และการเชื่อมต่อตัวเก็บประจุแบบขนานที่ส่วนหน้าของโหลด จะทำให้เกิดวงจรตัวกรองความถี่ต่ำผ่าน

ดังต่อไปนี้ ถ้า C1=1uF และ L1=22uH ระดับการลดทอนของวงจรกรองถึง
เป็นเท่าใด ส่วนประกอบ AC 100MHZ?

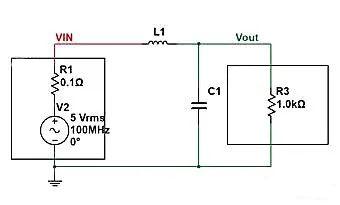
ณ จุดนี้ วงจรจะเชื่อมต่อแบบขนานกับอิมพีแดนซ์ Zc ของตัวเก็บประจุ (C1) และ R3 แล้วหารด้วยอิมพีแดนซ์ ZL ของตัวเหนี่ยวนำ (L1) ดังนั้นเราจึงสามารถแสดงรายการสมการอิมพีแดนซ์ได้ (ซึ่งเป็นสูตรตัวแบ่งแรงดันไฟฟ้าอนุกรมอย่างง่าย)

แอมพลิจูดการลดทอน=Vout/Vin=(Zc//R3)/(ZL+(Zc/R3)

ในจำนวนนั้น Zc=1/2 π fC และ ZL=2 π fL เมื่อให้ R3=1K Ω สรุปได้ว่า Zc=0.0015 Ω, Zc/R=0.00149 Ω

ZL=13816 Ω สามารถรับแอมพลิจูดการลดทอนได้เป็น 0.00149/(13816.00149)=0.000000178

จะเห็นได้ว่าส่วนประกอบ AC 100MHz แทบจะไม่สามารถผ่านวงจรกรองความถี่ต่ำผ่าน 22uH และ 1uF ได้ ในเวลาเดียวกัน เรายังเห็นว่าโหลด R3 อาจส่งผลต่อผลการกรองของตัวกรอง ดังนั้นบางครั้งเราพบว่าวงจรตัวกรองเดียวกันทำงานได้ดีบนวงจรนี้ แต่ทำงานได้ไม่ดีในวงจรอื่น